Co-Hub Node Based Multiview Graph Learning with Theoretical Guarantees

Identifying the graphical structure underlying the observed multivariate data is essential in numerous applications. Current methodologies are predominantly confined to deducing a singular graph under the presumption that the observed data are uniform. However, many contexts involve heterogeneous datasets that feature multiple closely related graphs, typically referred to as multiview graphs. Previous research on multiview graph learning promotes edge-based similarity across layers using pairwise or consensus-based regularizers. However, multiview graphs frequently exhibit a shared node-based architecture across different views, such as common hub nodes. Such commonalities can enhance the precision of learning and provide interpretive insight. In this paper, we propose a co-hub node model, positing that different views share a common group of hub nodes. The associated optimization framework is developed by enforcing structured sparsity on the connections of these co-hub nodes. Moreover, we present a theoretical examination of layer identifiability and determine bounds on estimation error. The proposed methodology is validated using both synthetic graph data and fMRI time series data from multiple subjects to discern several closely related graphs.

Robust Spatiotemporally Contiguous Anomaly Detection Using Tensor Decomposition

Anomaly detection in spatiotemporal data is a challenging problem encountered in a variety of applications, including video surveillance, medical imaging data, and urban traffic monitoring. Existing anomaly detection methods focus mainly on point anomalies and cannot deal with temporal and spatial dependencies that arise in spatio-temporal data. Tensor-based anomaly detection methods have been proposed to address this problem. Although existing methods can capture dependencies across different modes, they are primarily supervised and do not account for the specific structure of anomalies. Moreover, these methods focus mainly on extracting anomalous features without providing any statistical confidence. In this paper, we introduce an unsupervised tensor-based anomaly detection method that simultaneously considers the sparse and spatiotemporally smooth nature of anomalies. The anomaly detection problem is formulated as a regularized robust low-rank + sparse tensor decomposition where the total variation of the tensor with respect to the underlying spatial and temporal graphs quantifies the spatiotemporal smoothness of the anomalies. Once the anomalous features are extracted, we introduce a statistical anomaly scoring framework that accounts for local spatio-temporal dependencies. The proposed framework is evaluated on both synthetic and real data.

Learning Graph Filters for Structure-Function Coupling based Hub Node Identification

Over the past two decades, tools from network science have been leveraged to characterize the organization of both structural and functional networks of the brain. One such measure of network organization is hub node identification. Hubs are specialized nodes within a network that link distinct brain units corresponding to specialized functional processes. Conventional methods for identifying hub nodes utilize different types of centrality measures and participation coefficient to profile various aspects of nodal importance. These methods solely rely on the functional connectivity networks constructed from functional magnetic resonance imaging (fMRI), ignoring the structure-function coupling in the brain. In this paper, we introduce a graph signal processing (GSP) based hub detection framework that utilizes both the structural connectivity and the functional activation to identify hub nodes. The proposed framework models functional activity as graph signals on the structural connectivity. Hub nodes are then detected based on the premise that hub nodes are sparse, have higher level of activity compared to their neighbors, and the non-hub nodes' activity can be modeled as the output of a graph-based filter. Based on these assumptions, an optimization framework, GraFHub, is formulated to learn the coefficients of the optimal polynomial graph filter and detect the hub nodes. The proposed framework is evaluated on both simulated data and resting state fMRI (rs-fMRI) data from Human Connectome Project (HCP).

Multiview Graph Learning with Consensus Graph

Graph topology inference, i.e., learning graphs from a given set of nodal observations, is a significant task in many application domains. Existing approaches are mostly limited to learning a single graph assuming that the observed data is homogeneous. This is problematic because many modern datasets are heterogeneous or mixed and involve multiple related graphs, i.e., multiview graphs. Recent work proposing to learn multiview graphs ensures the similarity of learned view graphs through pairwise regularization, where each pair of views is encouraged to have similar structures. However, this approach cannot infer the shared structure across views. In this work, we propose an alternative method based on consensus regularization, where views are ensured to be similar through a learned consensus graph representing the common structure of the views. In particular, we propose an optimization problem, where graph data is assumed to be smooth over the multiview graph and the topology of the individual views and that of the consensus graph are learned, simultaneously. Our optimization problem is designed to be general in the sense that different regularization functions can be used depending on what the shared structure across views is. Moreover, we propose two regularization functions that extend fused and group graphical lasso to consensus based regularization. Proposed multiview graph learning is evaluated on simulated data and shown to have better performance than existing methods. It is also employed to infer the functional brain connectivity networks of multiple subjects from their electroencephalogram (EEG) recordings. The proposed method reveals the structure shared by subjects as well as the characteristics unique to each subject.

Optimal Graph Filters for Clustering Attributed Graphs

Many real-world systems can be represented as graphs where the different entities are presented by nodes and their interactions by edges. An important task in studying large datasets is graph clustering. While there has been a lot of work on graph clustering using the connectivity between the nodes, many real-world networks also have node attributes. Clustering attributed graphs requires joint modeling of graph structure and node attributes. Recent work has focused on graph convolutional networks and graph convolutional filters to combine structural and content information. However, these methods are mostly limited to lowpass filtering and do not explicitly optimize the filters for the clustering task. In this paper, we introduce a graph signal processing based approach, where we design polynomial graph filters optimized for clustering. The proposed approach is formulated as a two-step iterative optimization problem where graph filters that are interpretable and optimal for the given data are learned while maximizing the separation between different clusters. The proposed approach is evaluated on attributed networks and compared to the state-of-the-art graph convolutional network approaches.

From Nano to Macro: Overview of the IEEE Bio Image and Signal Processing Technical Committee

The Bio Image and Signal Processing (BISP) Technical Committee (TC) of the IEEE Signal Processing Society (SPS) promotes activities within the broad technical field of biomedical image and signal processing. Areas of interest include medical and biological imaging, digital pathology, molecular imaging, microscopy, and associated computational imaging, image analysis, and image-guided treatment, alongside physiological signal processing, computational biology, and bioinformatics. BISP has 40 members and covers a wide range of EDICS, including CIS-MI: Medical Imaging, BIO-MIA: Medical Image Analysis, BIO-BI: Biological Imaging, BIO: Biomedical Signal Processing, BIO-BCI: Brain/Human-Computer Interfaces, and BIO-INFR: Bioinformatics. BISP plays a central role in the organization of the IEEE International Symposium on Biomedical Imaging (ISBI) and contributes to the technical sessions at the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), and the IEEE International Conference on Image Processing (ICIP). In this paper, we provide a brief history of the TC, review the technological and methodological contributions its community delivered, and highlight promising new directions we anticipate.

Community Detection in Multi-frequency EEG Networks

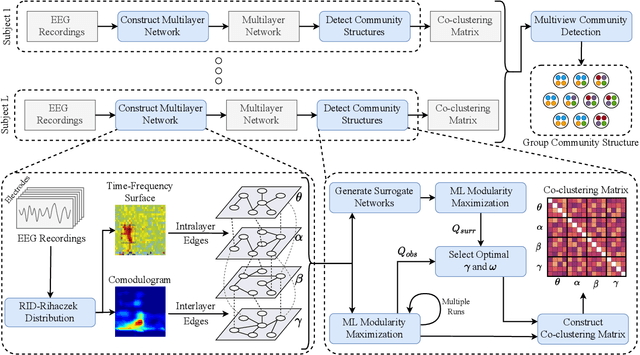
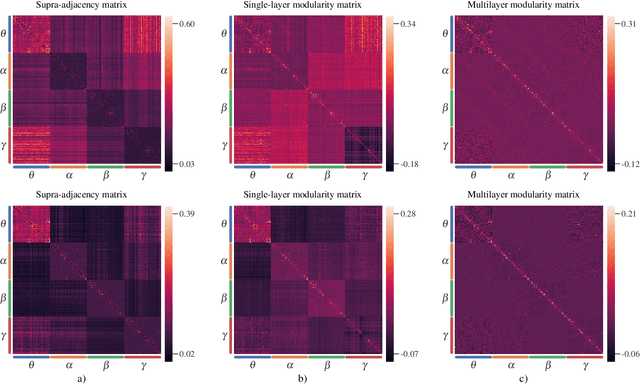
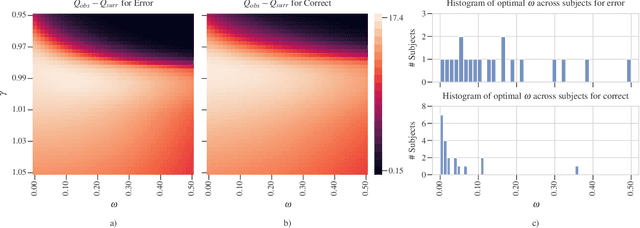
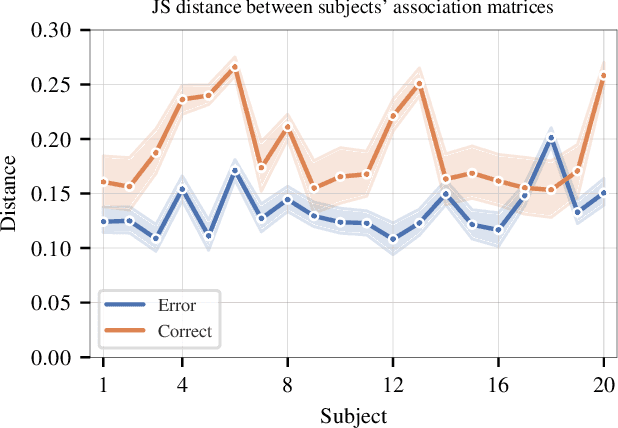
Objective: In recent years, the functional connectivity of the human brain has been studied with graph theoretical tools. One such approach is community detection which is fundamental for uncovering the localized networks. Existing methods focus on networks constructed from a single frequency band while ignoring multi-frequency nature of functional connectivity. Therefore, there is a need to study multi-frequency functional connectivity to be able to capture the full view of neuronal connectivity. Methods: In this paper, we use multilayer networks to model multi-frequency functional connectivity. In the proposed model, each layer corresponds to a different frequency band. We then extend the definition of modularity to multilayer networks to develop a new community detection algorithm. Results} The proposed approach is applied to electroencephalogram data collected during a study of error monitoring in the human brain. The differences between the community structures within and across different frequency bands for two response types, i.e. error and correct, are studied. Conclusion: The results indicate that following an error response, the brain organizes itself to form communities across frequencies, in particular between theta and gamma bands while a similar cross-frequency community formation is not observed for the correct response. Moreover, the community structures detected for the error response were more consistent across subjects compared to the community structures for correct response. Significance: The multi-frequency functional connectivity network models combined with multilayer community detection algorithms can reveal changes in cross-frequency functional connectivity network formation across different tasks and response types.

Community detection in multiplex networks based on orthogonal nonnegative matrix tri-factorization

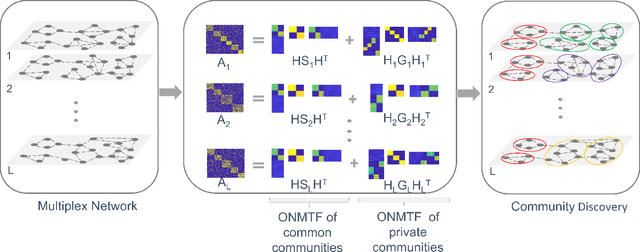
Networks provide a powerful tool to model complex systems where the different entities in the system are presented by nodes and their interactions by edges. Recently, there has been a growing interest in multiplex networks as they can represent the interactions between a pair of nodes through multiple types of links, each reflecting a distinct type of interaction. One of the important tools in understanding network topology is community detection. Although there are numerous works on community detection in single layer networks, existing work on multiplex community detection mostly focuses on learning a common community structure across layers without taking the heterogeneity of the different layers into account. In this paper, we introduce a new multiplex community detection approach that can identify communities that are common across layers as well as those that are unique to each layer. The proposed algorithm employs Orthogonal Nonnegative Matrix Tri-Factorization to model each layer's adjacency matrix as the sum of two low-rank matrix factorizations, corresponding to the common and private communities, respectively. The proposed algorithm is evaluated on both synthetic and real multiplex networks and compared to state-of-the-art techniques.

Coupled Support Tensor Machine Classification for Multimodal Neuroimaging Data

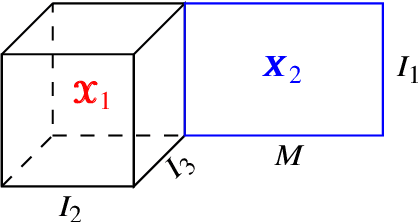
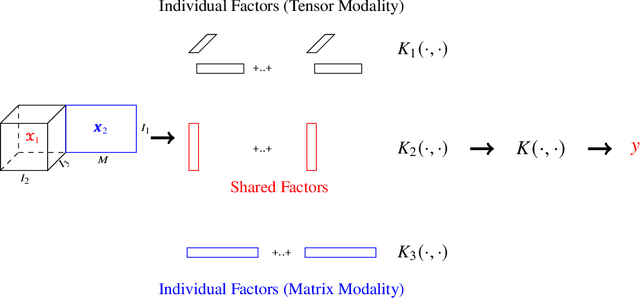
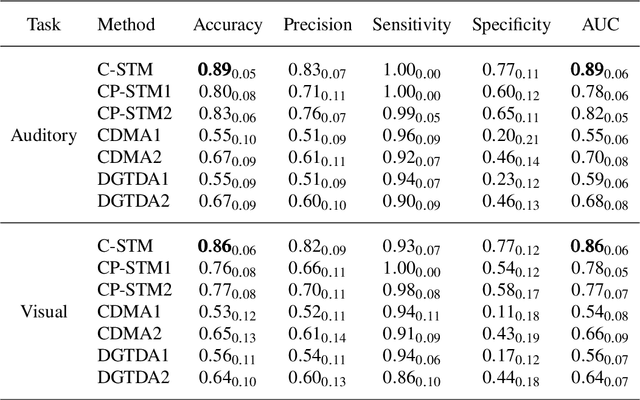
Multimodal data arise in various applications where information about the same phenomenon is acquired from multiple sensors and across different imaging modalities. Learning from multimodal data is of great interest in machine learning and statistics research as this offers the possibility of capturing complementary information among modalities. Multimodal modeling helps to explain the interdependence between heterogeneous data sources, discovers new insights that may not be available from a single modality, and improves decision-making. Recently, coupled matrix-tensor factorization has been introduced for multimodal data fusion to jointly estimate latent factors and identify complex interdependence among the latent factors. However, most of the prior work on coupled matrix-tensor factors focuses on unsupervised learning and there is little work on supervised learning using the jointly estimated latent factors. This paper considers the multimodal tensor data classification problem. A Coupled Support Tensor Machine (C-STM) built upon the latent factors jointly estimated from the Advanced Coupled Matrix Tensor Factorization (ACMTF) is proposed. C-STM combines individual and shared latent factors with multiple kernels and estimates a maximal-margin classifier for coupled matrix tensor data. The classification risk of C-STM is shown to converge to the optimal Bayes risk, making it a statistically consistent rule. C-STM is validated through simulation studies as well as a simultaneous EEG-fMRI analysis. The empirical evidence shows that C-STM can utilize information from multiple sources and provide a better classification performance than traditional single-mode classifiers.

Low-rank on Graphs plus Temporally Smooth Sparse Decomposition for Anomaly Detection in Spatiotemporal Data

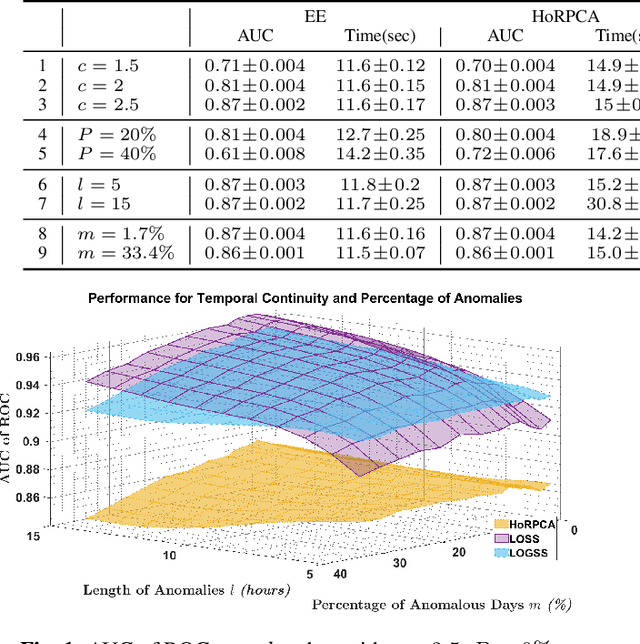
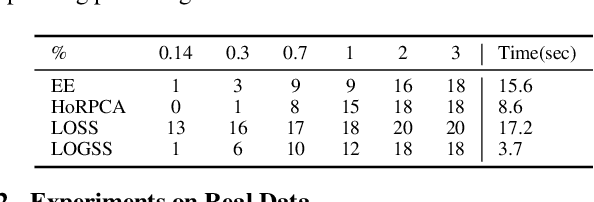
Anomaly detection in spatiotemporal data is a challenging problem encountered in a variety of applications including hyperspectral imaging, video surveillance, and urban traffic monitoring. Existing anomaly detection methods are most suited for point anomalies in sequence data and cannot deal with temporal and spatial dependencies that arise in spatiotemporal data. In recent years, tensor-based methods have been proposed for anomaly detection to address this problem. These methods rely on conventional tensor decomposition models, not taking the structure of the anomalies into account, and are supervised or semi-supervised. We introduce an unsupervised tensor-based anomaly detection method that takes the sparse and temporally continuous nature of anomalies into account. In particular, the anomaly detection problem is formulated as a robust lowrank + sparse tensor decomposition with a regularization term that minimizes the temporal variation of the sparse part, so that the extracted anomalies are temporally persistent. We also approximate rank minimization with graph total variation minimization to reduce the complexity of the optimization algorithm. The resulting optimization problem is convex, scalable, and is shown to be robust against missing data and noise. The proposed framework is evaluated on both synthetic and real spatiotemporal urban traffic data and compared with baseline methods.